Functional and in-place matrix rotation
December 23, 2015
In this post I’ll walk through rotating a bi-dimension matrix, in a functional way, by composing transpose and flip functions.
We’ll assume the matrix to be square (n*n).
Transpose a matrix
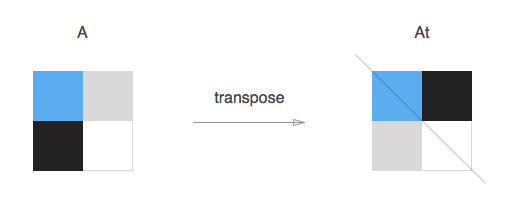
In linear algebra, the transpose of a matrix A is another matrix At created by reflecting A over its main diagonal (which runs from top-left to bottom-right) to obtain At. Formally, the i-th row, j-th column element of At is the j-th row, i-th column element of A:
A[j][i] === At[i][j];Therefore, a simple function to transpose a Matrix , returning a new transpose of the original, could look something like:
function transpose(matrix) {
var output = deepCopy(matrix);
for (var y = 0; y < matrix.length - 1; y++) {
for (var x = y + 1; x < matrix.length; x++) {
output[x][y] = matrix[y][x];
output[y][x] = matrix[x][y];
}
}
return output;
}We relied on a deepCopy helper to avoid side effects on the original Matrix. If you were seeking for a constant O(1) space complexity solution, scroll down for the in-place revised version.
Flip a Matrix
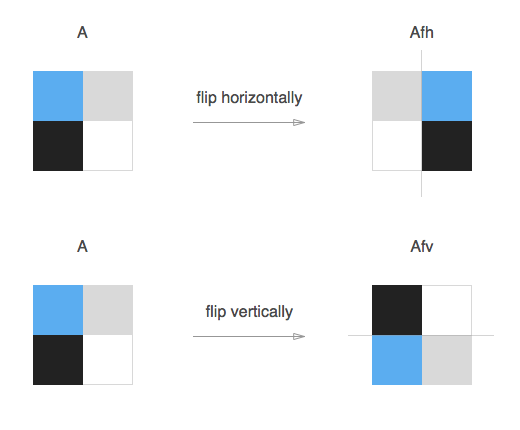
The horizontal flip of a matrix A is another matrix Afh created by reflecting A over its horizontal line of symmetry (which runs from mid-left to mid-right) to obtain Afh.
A[j][i] === Afh[j][A.length - 1 - i];While the vertical flip of a matrix A is another matrix Afv created by reflecting A over its vertical line of symmetry (which runs from mid-top to mid-bottom) to obtain Afv.
A[j][i] === Afv[A.length - 1 - j][i];Same idea, slightly different code:
function flipVertical(matrix) {
var output = deepCopy(matrix);
for (var y = 0; y < (output.length - 1)/ 2; y++) {
for (var x = 0; x < output.length; x++) {
output[y][x] = matrix[matrix.length-1-y][x];
output[output.length-1-y][x] = matrix[y][x];
}
}
return output;
}function flipHorizontal(matrix) {
var output = deepCopy(matrix);
for (var y = 0; y < matrix.length; y++) {
for (var x = 0; x < (matrix.length - 1)/2; x++) {
output[y][x] = matrix[y][matrix.length - 1 - x];
output[y][matrix.length - 1 - x] = matrix[y][x];
}
}
return output;
}Rotating
At this point rotating the Matrix, is just a matter of function composition:
- rotate 90 degree clock wise = flipHorizontal(transpose(matrix))
- rotate 90 degree counter clock wise = flipVertical(transpose(matrix))
- rotate 180 degree = flipVertical(flipHorizontal(matrix))
We could then put it all together and have a pretty sweet Matrix rotating function:
function rotateMatrix(matrix, deg) {
deg = deg || 90;
switch(deg) {
case 90:
return flipHorizontal(transpose(matrix));
case -90:
return flipVertical(transpose(matrix));
case 180:
return flipVertical(flipHorizontal(matrix));
case 270:
return flipVertical(transpose(matrix));
case -270:
return flipHorizontal(transpose(matrix));
}
}In-place rotation
You are tight in memory and desperately need that O(1) space implementation? Here we go, it will be just a matter of slightly tweaking our transpose and flip functions so that they operate in-place:
function transposeInPlace(matrix) {
for (var y = 0; y < matrix.length - 1; y++) {
for (var x = y + 1; x < matrix.length; x++) {
var temp = matrix[x][y];
matrix[x][y] = matrix[y][x];
matrix[y][x] = temp;
}
}
return matrix;
}
function flipVerticalInPlace(matrix) {
for (var y = 0; y < (matrix.length - 1)/ 2; y++) {
for (var x = 0; x < matrix.length; x++) {
var temp = matrix[y][x];
matrix[y][x] = matrix[matrix.length-1-y][x];
matrix[matrix.length-1-y][x] = temp;
}
}
return matrix;
}
function flipHorizontalInPlace(matrix) {
for (var y = 0; y < matrix.length; y++) {
for (var x = 0; x < (matrix.length - 1)/2; x++) {
var temp = matrix[y][x];
matrix[y][x] = matrix[y][matrix.length - 1 - x];
matrix[y][matrix.length - 1 - x] = temp;
}
}
return matrix;
}
function rotateMatrixInPlace(matrix, deg) {
deg = deg || 90;
switch(deg) {
case 90:
return flipHorizontalInPlace(transposeInPlace(matrix));
case -90:
return flipVerticalInPlace(transposeInPlace(matrix));
case 180:
return flipVerticalInPlace(flipHorizontalInPlace(matrix));
case 270:
return flipVerticalInPlace(transposeInPlace(matrix));
case -270:
return flipHorizontalInPlace(transposeInPlace(matrix));
}
}