DepthFirst and breadthFirst tree walking

Depth-first search (DFS) and Breadth-first search (BFS) are algorithms for traversing or searching tree or graph data structures.

While both starts at the root, DFS explores as far as possible along each branch before backtracking while BFS explores the neighbor nodes first, before moving to the next level neighbors.

Visualizing the algorithms

Assuming that an instance of a binary search tree hold some values, we can visualize the two traversing algorithms as following:

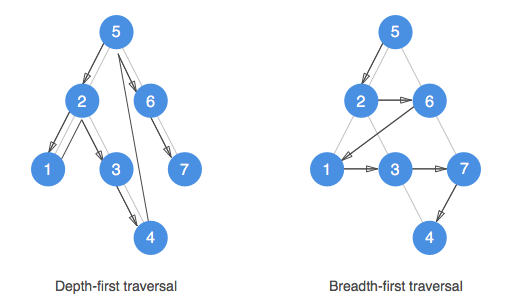
One pseudocode to rule them all

Although the algorithms may seems different, both share the “same” pseudocode:

// <store> the root node in a <container>
// While (the <container> isn't empty)
//   el = the <next> element from the container
//   <store> all the children of el in the container
//   do something with el 

What is happening here is that every time we get out of the container a node that we stored in there earlier, we unwrap its children and store each of them back into the container, moving on unitl we don’t have any more nodes in it. All the logic is therefore delegated to the <container>, and how the container <store> and retrive the <next> element (that in our case will be a tree node).

####DFS: replace <container> with stack

In the case of a DFS where we want to explore as far as possible along each branch before backtracking, a stack will be the perfect candidate for implementing our <container>. Thanks to its LIFO (Last-In-First-Out) approach, every time we’ll pop the <next> element it will be a direct a child of the branch we are traversing, or in the case we reached the end of a branch, a backtracked node up in the branch, where the branch forked out. As soon as we encounter a node that allow us to explore deeper we’ll move into that branch and explore it till we reach its end, before strarting to backtrack again. And so on until we traversed the whole tree.

      Given the following binary search tree:

0             (5)
             /   \
            /     \
1         (2)     (6)
         /   \       \
        /     \       \
2     (1)     (3)     (7)
                 \
                  \
3                 (4)

      // Traversing the tree using DFS may result in 
      // encountering each of its nodes in the following order:
      // ->  [ 5, 2, 1, 3, 4, 6, 7 ]

####BFS: replace <container> with queue

In the case of a BFS where we want to explore the neighbor nodes first, before moving to a depper level of the tree, a queue will be the perfect candidate for implementing our <container>. Thanks to its FIFO (First-In-First-Out) approach, every time we’ll dequeue the <next> element it will be a neighbour node, or, in the case we visited all of the neighbours for that specific depth of the tree, the first node in the next level.And so on until we traversed the whole tree.

      Given the following binary search tree:

0             (5)
             /   \
            /     \
1         (2)     (6)
         /   \       \
        /     \       \
2     (1)     (3)     (7)
                 \
                  \
3                 (4)

      // Traversing the tree using BFS may result in 
      // encountering each of its nodes in the following order:
      // ->  [ 5, 2, 6, 1, 3, 7, 4 ]

Depth-first and Breadth-first search implementation

Let’s assume we have stacks and queues implemented (in js, we could easily get along by just relying to array and its native methods push/pop for stacks and push/shift for queues). We could then immagine a depthFirstLog() and breadthFirstLog() methods for a binary search tree to be like:

BinarySearchTree.prototype.depthFirstLog = function(cb) {
  var container = new Stack(); 
  var element;

  container.push(this);
  while (container.size() > 0) {  
    element = container.pop();

    if (element._right) {
      container.push(element._right);
    }
    if (element._left) {
      container.push(element._left);
    }
    cb(element._value);
  }
};

BinarySearchTree.prototype.breadthFirstLog = function(cb) {
  var container = new Queue(); 
  var element;

  container.enqueue(this);
  while (container.size() > 0) {  
    element = container.dequeue();
    if (element._left) {
      container.enqueue(element._left);
    }
    if (element._right) {
      container.enqueue(element._right);
    }
    cb(element._value);
  }
};

Alternatively, we could mimic how stacks works using a recursive approach. A recursive solution in that direction may look something like:

BinarySearchTree.prototype.depthFirstLog = function(cb) {
  cb(this._value);
  if (this._left) {
    this._left.depthFirstLog(cb);
  }
  if (this._right) {
    this._right.depthFirstLog(cb);
  }
};

##Final thoughts

I found mastering DFS and BFS algorithms to be very beneficial for solving many tree traversing problems.

Rely on Depth-first (DFS) if:

• Searched items are deep inside the tree
• Finding the shortest path from the root is not an issue
• Space complexity is an important factor
  
  

Rely on Breadth-first (BFS) if:

• Searched item is not far from the root node
• Finding the shortest path from the root is important
• Space complexity is not an important factor